Solving Geometric Problems – Tips And Tricks

Geometry is fun and even more fun when you score the desired marks. With only a set of rules and theorems to memorize, you are on your way of earning the grades you have always wished for.

Another important part of the tricks is to be ready and eager to draw as many figures as possible. When you draw the right figures, you will definitely remember the right property of the triangle in question.

Thus, pick up your pencil and scribble away. Do not be tempted to disregard the drawing step just because the question has provided you with one. Make sure you draw yours as this is a key step in understanding the problem.

Different methods of solving problems with triangles include the Pythagoras Theorem. You must be conversant with the theorem ‘Soh-Cah-toa’ by now. Perhaps you are wondering why it is so important in geometry. Before you proceed to practice a few questions on your own or with the help of a Geometry Tutor, you must be certain about the formula to consider.

1. The type of triangle involved – This is especially important because it goes a long way in determining the right formula for the specific question. Therefore, classify the triangle in question.
2. Missing angles or missing sides? – Whether angle or side, each part of the triangle has a dedicated formula.
3. Special cases in different triangles – There are different right triangles with differing methods of calculation. Take note of this so that you are well guided.

Method 1 – Classification of the triangle

You can classify the triangle by the number of sides it contains. By so doing, every class of triangle will have a specific formula. The classification goes thus:

1. The number of sides – In Latin, ‘tri’ means ‘three’. Therefore, a triangle infers an object with three sides and matching angles (three). Like everyone has a name and surname to differentiate them from people of the same first name, triangles are classified as such.

• A triangle with all sides equal is called an ‘equilateral’ triangle.
• A triangle with two equal sides is called an ‘isosceles’ triangle.
• A triangle with no equal sides is called a ‘scalene’ triangle.

2. The number of angles – For every triangle, there is a special way to classify them based on the number of angles present.

• A right-angled triangle has one 90 degrees angle.
• An acute triangle has angles which are less than 90 degrees.
• An obtuse triangle has one of its angles greater than 90 degrees.

Method 2 – Solving missing sides in a right-angled triangle

This is the part that is mostly affected by the ‘Pythagoras Theorem’. You should know that right-angled triangles are special triangles. Because of the presence of one 90 degrees angle, you will require fewer steps to get the right solution. Surprisingly, there are three different formulas of solving for missing angles and sides.

1. Pythagoras theorem – This formula is used to solve for missing sides. Let us consider a hypothetical right-angled triangle:

 

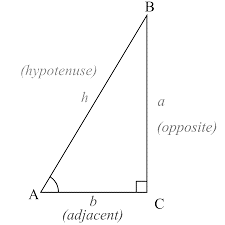
Here, Pythagoras Theorem states that:

While this is a straightforward method of solving the problem, there are more ways to solve for missing sides which seem tricky.

2. A 30-60-90 triangle – This means that the right-angled triangle has another angle inclusive. Depending on the angle contained, it may be either 30 degrees, 60 degrees, or 90 degrees. That said, there is always a special ratio applicable to solving the problem.

• The side which corresponds to 30 degrees will be 1.
• The side which corresponds to 60 degrees will be
• The side which corresponds to 90 degrees will be 2

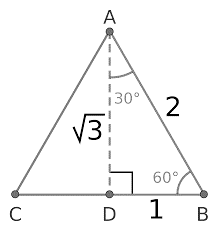
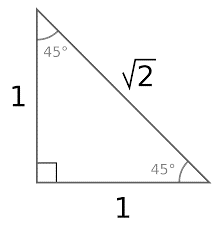
3. A 45-45-90 triangle – This shows that the triangle has two sides which are equal. Thus, it can be called an isosceles triangle. Just like the first special triangle, this will be:

• The side corresponding to the 45-degree angle will be 1.
• The side corresponding to the 45-degree angle will be 1.
• The side corresponding to 90 degrees will be

Method 3 – Solve for missing angles in a right-angled triangle

Once we know the side, the missing angle is always easy to discover. The trick here is to remember that a triangle always has ‘three’ sides and the next step is to calculate the ratio between corresponding angles and sides. For this, there are three formulas as well. Study the triangle below after which we will infer the trigonometric ratio.

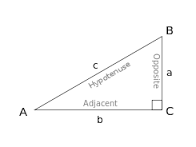
Starting from angle A:

• Hypotenuse – longest side of the triangle and it is denoted by side ‘c’ and angle ‘C’
• Opposite side – the side opposite our point of interest angle ‘A’ and denoted by side ‘a’
• Adjacent side – side next to the original angle and denoted by side ‘b’.?

Post Tags EducationLearningMathGeometryStudy Tips